73 Data Structure Interview Questions and Answers

What is hashing technique? Describe in brief.

In general, in all searching techniques, search time is dependent on the number of items. Sequential search, binary search and all the search trees are totally dependent on number of items and many key comparisons are involved.

Hashing is a technique where search time is independent of the number of items or elements. In this technique a hash function is used to generate an address from a key. The hash function takes a key as input and returns the hash value of that key which is used as an address index in the array.



We can write hash function as follows
h(k)=a;

Where h is hash function, k is the key, a is the hash value of the key.

While choosing a hash function we should consider some important points.
- It should be easy to compute
- It should generate address with minimum collision.

What are different techniques for making hash function? Explain with example.

Techniques for making hash function.
- Truncation Method
- Midsquare Method
- Folding Method
- Division Method

Truncation Method
This is the simplest method for computing address from a key.In this method we take only a part of the key as address.

Example:
Let us take some 8 digit keys and find addresses for them. Let the table size is 100 and we have to take 2 rightmost digits for getting the hash table address. Suppose the keys are. 62394572,87135565,93457271,45393225.

So the address of above keys will be 72,65,71 and 25 respectively.

This method is easy to compute but chances of collision are more because last two digits can be same in more than one keys.

Midsquare Method
In this method the key is squared and some digits from the middle of this square are taken as address.

Example:
Suppose that table size is 1000 and keys are as follows

Key	1123	2273	3139	3045
Square of key	1261129	5166529	9853321	9272025
Address	612	665	533	720

Folding Method
In this technique the key is divided into different part where the length of each part is same as that of the required address, except possibly the last part.

Example:
Let key is 123945234 and the table size is 1000 then we will broke this key as follows

123945234 ----> 123 945 234

Now we will add these broken parts. 123+945+234=1302. The sum is 1302, we will ignore the final carry 1, so the address for the key 123945234 is 302.

Division Method (Modulo-Division)
In Modulo-Division method the key is divided by the table size and the remainder is taken as the address of the hash table.

Let the table size is n then

H (k) =k mod n

Example

Let the keys are 123, 945,234 and table size is 11 then the address of these keys will be.

123 % 11=2
945%11=10
235%11=4

So the hash address of above keys will be 2,10,4.

Note: - Collisions can be minimized if the table size is taken to be a prime number.

What are different methods of collision resolution in hashing.

A collision occurs whenever a key is mapped to an address that is already occupied. Collision Resolution technique provides an alternate place in hash table where this key can be placed.

Collision Resolution technique can be classified as:
1) Open Addressing (Closed Hashing)
a) Linear Probing
b) Quadratic Probing
c) Double Hashing

2) Separate Chaining (Open Hashing)

Describe Linear Probing with an example.

In this method if address given by hash function is already occupied, then the key will be inserted in the next empty position in hash table. Let the table size is 7 and hash function returns address 4 for a key then we will search the empty location in this sequence.

4, 5, 6, 7, 0, 1, 2, 3

Example:
Let the keys are 28, 47, 20, 36, 43, 23, 25, 54 and table size is 11 then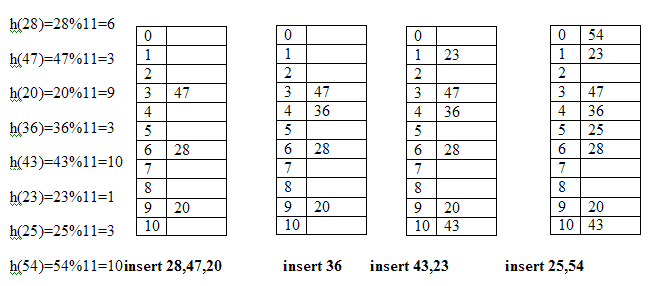

Describe the following term in a tree.

a) Level b) Height c) Degree.

Let’s take an example to define the above term.



Level:
Level of any node is defined as the distance of that node from the root. The level of root node is always zero. Node B, C, M, E are at level 1.Nodes K,G,H,I,J,F,L are at level 2.Nodes A,N,O,P,D,S are at level 3.

Height:
Height is also known as depth of the tree. The height of root node is one. Height of a tree is equal to one more than the largest level number of tree. The height of the above tree is 4.

Degree:
The number of children of a node is called its degree. The degree of node R is 4, the degree of node B is 3.The degree of node S is 0.The degree of a tree is the maximum degree of the node of the tree. The degree of the above given tree is 4.

Describe binary tree and its property.

In a binary tree a node can have maximum two children, or in other words we can say a node can have 0,1, or 2 children.

Properties of binary tree.

1) The maximum number of nodes on any level i is 2ⁱ where i>=0.

2) The maximum number of nodes possible in a binary tree of height h is 2^h-1.

3) The minimum number of nodes possible in a binary tree of height h is equal to h.

4) If a binary tree contains n nodes then its maximum possible height is n and minimum height possible is log₂ (n+1).

5) If n is the total no of nodes and e is the total no of edges then e=n-1.The tree must be non-empty binary tree.

6) If n₀ is the number of nodes with no child and n₂ is the number of nodes with 2 children, then n₀=n₂+1.

Describe full binary tree and complete binary tree.

Full binary tree: A binary tree is full binary tree if all the levels have maximum number of nodes.

A full binary tree of height h has (2^h– 1) nodes.

Complete binary tree:In a complete binary tree all the levels have maximum number of nodes except possibly the last level.

The minimum no of nodes in a complete binary tree is 2^h-1 and the maximum number of nodes possible is (2^h– 1).Where h is the height of the tree.

Explain Extended Binary tree.

A binarytree can be converted to an extended binary tree by adding special nodes to leaf nodes and nodes that have only one child.Extended binary tree is also called 2-tree.



In the above figure external nodes are shown by squares and internal nodes by circles. The extended binary tree is a strictly binary tree means each node has either 0 or 2 children. The path length of any node is the number of edges traversed from that node to the root node. Internal path length of a binary tree is the sum of path lengths of all internal nodes and external path length of a binary tree is the sum of path lengths of all external nodes.

What are different dynamic memory allocation technique in C .

The process of allocating memory at run time is called dynamic memory allocation. The allocation and release of this memory space can be done with the help of some predefined function. These functions allocate memory from a memory area called heap and free this memory whenever not required.

The functions that are used to allocate memory at runtime are as follows:
- malloc()
- calloc()
- realloc()

1. malloc()
This function allocates memory dynamically.

It is generally used as:Here ptr is a pointer of type datatype ( can be int, float, double….) and specified size is the size in bytes. The expression (datatype *) is used to typecast the pointer returned by malloc().

Example:It allocates the memory space to hold four integer values and the address of first byte is stored in the pointer variable ptr. The allocated memory contains garbage value.

2. calloc()
The calloc() function is used to allocate multiple blocks of memory.

Example:It allocates 4 blocks of memory and each block contains 2 bytes.

3. realloc()
We can increase or decrease the memory allocated by malloc() or calloc() function. The realloc() function is used to change the size of the memory block. It changes the memory block without destroying the old data.

Example:This function takes two argument, first is a pointer to the block of memory that was previously allocated by malloc() or calloc() and second argument is the new size of memory block.

What are the difference between malloc() and calloc()?

Following are the main difference between malloc() and calloc().

- calloc() function takes two parameters but malloc() function takes only one parameter.

- Memory allocated by calloc() is initialized to zero while memory allocated by malloc() contains garbage value.

How will you free the memory that is allocated at run time?

Memory is one of the most important resources and it is limited. The dynamically allocated memory is not automatically released; it will exist till the end of program. So it is programmer’s responsibility to free the memory after completion. The free() function is used to release the memory that is allocated at run time.

Example:Here ptr is a pointer variable that contains the base address of a memory block created by malloc() or calloc() function.

What are different application of stack.

Some of the applications of stack are as follows:
- Function calls.
- Reversal of a string.
- Checking validity of an expression containing nested parenthesis.
- Conversion of infix expression to postfix.

How will you check the validity of an expression containing nested parentheses?

One of the applications of stack is checking validity of an expression containing nested parenthesis. An expression will be valid if it satisfies the two conditions.

- The total number of left parenthesis should be equal to the total number of right parenthesis in the expression.

- For every right parenthesis there should be a left parenthesis of the same time.

The procedure for checking validity of an expression containing nested parenthesis:
1. First take an empty stack
2. Scan the symbols of expression from left to right.
3. If the symbol is a left parenthesis then push it on the stack.
4. If the symbol is right parenthesis then
            If the stack is empty then the expression is invalid because Right parentheses are more
            than left parenthesis.
            else
            Pop an element from stack.
            If popped parenthesis does not match the parenthesis being scanned then it is invalid
            because of mismatched parenthesis.

5. After scanning all the symbols of expression, if stack is empty then expression is valid else it is invalid because left parenthesis is more than right parenthesis.

Describe AVL tree or height balanced binary search tree.

An AVL tree is binary search tree (BST) where the difference in the height of left and right subtrees of any node can be at most one. The technique for balancing the binary search tree was introduced by Russian Mathematicians G. M. Adelson and E. M. Landis in 1962. The height balanced binary search tree is called AVL tree in their honor.

Example:



For the leaf node 12, 40, 65 and 98 left and right subtrees are empty so difference of heights of their subtrees is zero.

For node 20 height of left subtree is 2 and height of right subtree is 3 so difference is 1.

For node 15 height of left subtree is 1 and height of right subtree is 0 so difference is 1.

For node 57 height of left subtree is 1 and height of right subtree is 2 so difference is 1.

For node 78 height of left subtree is 1 and height of right subtree is 1 so difference is 0.

Each node of an AVL tree has a balance factor, which is defined as the difference between the heights of left subtree and right subtree of a node.

Balance factor of a node=Height of its left subtree - Height of its right subtree.

In AVL tree possible values for the balance factor of any node are -1, 0, 1.

Describe Tree Rotation in AVL tree.

After insertion or deletion operation the balance factor of the nodes in AVL tree can be changed and the tree may not be balanced. We can balance this tree by performing tree rotations. We know that AVL tree is binary search tree. Rotation of the tree should be in such a way that the new converted tree maintain the binary search tree property with inorder traversal same as that of the original tree.

There are two types of tree rotation
- Right Rotation
- Left Rotation



Fig: Right Rotation

Give one example of Right Rotation.

Right Rotation about node 25.

What is Data Structure?

- Data structure is a group of data elements grouped together under one name.
- These data elements are called members. They can have different types and different lengths.
- Some of them store the data of same type while others store different types of data.

Which data structure is used to perform recursion?

- The data structure used for recursion is Stack.
- Its LIFO property helps it remembers its 'caller'. This helps it know the data which is to be returned when the function has to return.
- System stack is used for storing the return addresses of the function calls.

Does the Minimal Spanning tree of a graph give the shortest distance between any 2 specified nodes?

- No, it doesn’t.
- It assures that the total weight of the tree is kept to minimum.
- It doesn't imply that the distance between any two nodes involved in the minimum-spanning tree is minimum.

If you are using C language to implement the heterogeneous linked list, what pointer type will you use?

- A heterogeneous linked list contains different data types in its nodes. We can not use ordinary pointer to connect them.
- The pointer that we use in such a case is void pointer as it is a generic pointer type and capable of storing pointer to any type.

Differentiate between PUSH and POP?

- Pushing and popping refers to the way data is stored into and retrieved from a stack.
- PUSH – Data being pushed/ added to the stack.
- POP - Data being retrieved from the stack, particularly the topmost data.

When is a binary search algorithm best applied?

- It is best applied to search a list when the elements are already in order or sorted.
- The list here is searched starting in the middle. If that middle value is not the correct one, the lower or the upper half is searched in the similar way.

How do you reference all the elements in a one-dimension array?

- This is done using an indexed loop.
- The counter runs from 0 to the array size minus one.
- Using the loop counter as the array subscript helps in referencing all the elements in one-dimensional array.

What is Huffman’s algorithm?

- It is used in creating extended binary trees that have minimum weighted path lengths from the given weights.
- It makes use of a table that contains frequency of occurrence for each data element.

What is Fibonacci search?

- It is a search algorithm that applies to a sorted array.
- It uses divide-and-conquer approach that reduces the time needed to reach the target element.

Which data structure is applied when dealing with a recursive function?

- A recursive function is a function that calls itself based on a terminating condition.
- It uses stack.
- Using LIFO, a call to a recursive function saves the return address. This tells the return address to the calling function after the call terminates.

How does dynamic memory allocation help in managing data?

- Dynamic memory allocation helps to store simple structured data types.
- It can combine separately allocated structured blocks to form composite structures that expand and contract as required.

What is a bubble sort and how do you perform it?

- Bubble sort is a sorting technique which can be applied to data structures like arrays.
- Here, the adjacent values are compared and their positions are exchanged if they are out of order.
- The smaller value bubbles up to the top of the list, while the larger value sinks to the bottom.

How does variable declaration affect memory allocation?

- The amount of memory to be allocated depends on the data type of the variable.
- An integer type variable is needs 32 bits of memory storage to be reserved.

You want to insert a new item in a binary search tree. How would you do it?

- Let us assume that the you want to insert is unique.
- First of all, check if the tree is empty.
- If it is empty, you can insert the new item in the root node.
- If it is not empty, refer to the new item’s key.
- If the data to be entered is smaller than the root’s key, insert it into the root’s left subtree.
- Otherwise, insert it into the root’s right subtree.

Why is the isEmpty() member method called?

- The isEmpty() member method is called during the dequeue process. It helps in ascertaining if there exists any item in the queue which needs to be removed.
- This method is called by the dequeue() method before returning the front element.

What is a queue ?

- A Queue refers to a sequential organization of data.
- It is a FIFO type data structure in which an element is always inserted at the last position and any element is always removed from the first position.

What is adequeue?

- A dequeue is a double-ended queue.
- The elements here can be inserted or removed from either end.

What is a postfix expression?

- It is an expression in which each operator follows its operands.
- Here, there is no need to group sub-expressions in parentheses or to consider operator precedence..

What is a data structure? What are the types of data structures? Briefly explain them

The scheme of organizing related information is known as ‘data structure’.

The types of data structure are:
Lists: A group of similar items with connectivity to the previous or/and next data items.
Arrays: A set of homogeneous values
Records: A set of fields, where each field consists of data belongs to one data type.
Trees: A data structure where the data is organized in a hierarchical structure. This type of data structure follows the sorted order of insertion, deletion and modification of data items.
Tables: Data is persisted in the form of rows and columns. These are similar to records, where the result or manipulation of data is reflected for the whole table.

Define a linear and non linear data structure.

Linear data structure: A linear data structure traverses the data elements sequentially, in which only one data element can directly be reached. Ex: Arrays, Linked Lists

Non-Linear data structure: Every data item is attached to several other data items in a way that is specific for reflecting relationships. The data items are not arranged in a sequential structure. Ex: Trees, Graphs

Define in brief an array. What are the types of array operations?

An array is a set of homogeneous elements. Every element is referred by an index.

Arrays are used for storing the data until the application expires in the main memory of the computer system. So that, the elements can be accessed at any time.

The operations are:
- Adding elements
- Sorting elements
- Searching elements
- Re-arranging the elements
- Performing matrix operations
- Pre-fix and post-fix operations

What is a matrix? Explain its uses with an example

A matrix is a representation of certain rows and columns, to persist homogeneous data. It can also be called as double-dimensioned array.

Uses:
- To represent class hierarchy using Boolean square matrix
- For data encryption and decryption
- To represent traffic flow and plumbing in a network
- To implement graph theory of node representation

Define an algorithm. What are the properties of an algorithm? What are the types of algorithms?

Algorithm: A step by step process to get the solution for a well defined problem.

Properties of an algorithm:
- Should be written in simple English
- Should be unambiguous, precise and lucid
- Should provide the correct solutions
- Should have an end point
- The output statements should follow input, process instructions
- The initial statements should be of input statements
- Should have finite number of steps
- Every statement should be definitive

Types of algorithms:
– Simple recursive algorithms. Ex: Searching an element in a list
– Backtracking algorithms Ex: Depth-first recursive search in a tree
– Divide and conquer algorithms. Ex: Quick sort and merge sort
– Dynamic programming algorithms. Ex: Generation of Fibonacci series
– Greedy algorithms Ex: Counting currency
– Branch and bound algorithms. Ex: Travelling salesman (visiting each city once and minimize the total distance travelled)
– Brute force algorithms. Ex: Finding the best path for a travelling salesman
– Randomized algorithms. Ex. Using a random number to choose a pivot in quick sort).

What is an iterative algorithm?

The process of attempting for solving a problem which finds successive approximations for solution, starting from an initial guess. The result of repeated calculations is a sequence of approximate values for the quantities of interest.

What is an recursive algorithm?

Recursive algorithm is a method of simplification that divides the problem into sub-problems of the same nature. The result of one recursion is the input for the next recursion. The repletion is in the self-similar fashion. The algorithm calls itself with smaller input values and obtains the results by simply performing the operations on these smaller values. Generation of factorial, Fibonacci number series are the examples of recursive algorithms.

Explain quick sort and merge sort algorithms.

Quick sort employs the ‘divide and conquer’ concept by dividing the list of elements into two sub elements.

The process is as follows:
1. Select an element, pivot, from the list.
2. Rearrange the elements in the list, so that all elements those are less than the pivot are arranged before the pivot and all elements those are greater than the pivot are arranged after the pivot. Now the pivot is in its position.
3. Sort the both sub lists – sub list of the elements which are less than the pivot and the list of elements which are more than the pivot recursively.

Merge Sort: A comparison based sorting algorithm. The input order is preserved in the sorted output.

Merge Sort algorithm is as follows:
1. The length of the list is 0 or 1, and then it is considered as sorted.
2. Other wise, divide the unsorted list into 2 lists each about half the size.
3. Sort each sub list recursively. Implement the step 2 until the two sub lists are sorted.
4. As a final step, combine (merge) both the lists back into one sorted list.

What is Bubble Sort and Quick sort?

Bubble Sort: The simplest sorting algorithm. It involves the sorting the list in a repetitive fashion. It compares two adjacent elements in the list, and swaps them if they are not in the designated order. It continues until there are no swaps needed. This is the signal for the list that is sorted. It is also called as comparison sort as it uses comparisons.

Quick Sort: The best sorting algorithm which implements the ‘divide and conquer’ concept. It first divides the list into two parts by picking an element a ’pivot’. It then arranges the elements those are smaller than pivot into one sub list and the elements those are greater than pivot into one sub list by keeping the pivot in its original place.

What are the difference between a stack and a Queue?

Stack – Represents the collection of elements in Last In First Out order.
Operations includes testing null stack, finding the top element in the stack, removal of top most element and adding elements on the top of the stack.

Queue - Represents the collection of elements in First In First Out order.

Operations include testing null queue, finding the next element, removal of elements and inserting the elements from the queue.

Insertion of elements is at the end of the queue

Deletion of elements is from the beginning of the queue.

Can a stack be described as a pointer? Explain.

A stack is represented as a pointer. The reason is that, it has a head pointer which points to the top of the stack. The stack operations are performed using the head pointer. Hence, the stack can be described as a pointer.

Explain the terms Base case, Recursive case, Binding Time, Run-Time Stack and Tail Recursion.

Base case: A case in recursion, in which the answer is known when the termination for a recursive condition is to unwind back.

Recursive Case: A case which returns to the answer which is closer.

Run-time Stack: A run time stack used for saving the frame stack of a function when every recursion or every call occurs.

Tail Recursion: It is a situation where a single recursive call is consisted by a function, and it is the final statement to be executed. It can be replaced by iteration.

Is it possible to insert different type of elements in a stack? How?

Different elements can be inserted into a stack. This is possible by implementing union / structure data type. It is efficient to use union rather than structure, as only one item’s memory is used at a time.

Explain in brief a linked list.

A linked list is a dynamic data structure. It consists of a sequence of data elements and a reference to the next record in the sequence. Stacks, queues, hash tables, linear equations, prefix and post fix operations. The order of linked items is different that of arrays. The insertion or deletion operations are constant in number.

Explain the types of linked lists.

The types of linked lists are:
Singly linked list: It has only head part and corresponding references to the next nodes.

Doubly linked list: A linked list which both head and tail parts, thus allowing the traversal in bi-directional fashion. Except the first node, the head node refers to the previous node.

Circular linked list: A linked list whose last node has reference to the first node.

How would you sort a linked list?

Step 1: Compare the current node in the unsorted list with every element in the rest of the list. If the current element is more than any other element go to step 2 otherwise go to step 3.

Step 2: Position the element with higher value after the position of the current element. Compare the next element. Go to step1 if an element exists, else stop the process.

Step 3: If the list is already in sorted order, insert the current node at the end of the list. Compare the next element, if any and go to step 1 or quit.

What is sequential search? What is the average number of comparisons in a sequential search?

Sequential search: Searching an element in an array, the search starts from the first element till the last element.

The average number of comparisons in a sequential search is (N+1)/2 where N is the size of the array. If the element is in the 1st position, the number of comparisons will be 1 and if the element is in the last position, the number of comparisons will be N.

What are binary search and Fibonacci search?

Binary Search: Binary search is the process of locating an element in a sorted list. The search starts by dividing the list into two parts. The algorithm compares the median value. If the search element is less than the median value, the top list only will be searched, after finding the middle element of that list. The process continues until the element is found or the search in the top list is completed. The same process is continued for the bottom list, until the element is found or the search in the bottom list is completed. If an element is found that must be the median value.

Fibonacci Search: Fibonacci search is a process of searching a sorted array by utilizing divide and conquer algorithm. Fibonacci search examines locations whose addresses have lower dispersion. When the search element has non-uniform access memory storage, the Fibonacci search algorithm reduces the average time needed for accessing a storage location.

What is the method to find the complexity of an algorithm?

Complexity of an algorithm can be found out by analyzing the resources like memory, processor, etc. The computational time is also used to find the complexity of an algorithm. The running time through which the program is processed requires the function of the size of the input. The complexity is measured by number of steps that has to be executed for a particular input. The space complexity and the time complexity are the two main methods which allow the user to know the complexity of the algorithm and allow user to make it more optimized.

What is the use of space complexity and time complexity?

The space complexity defines the storage capacity for the input data. It defines the amount of memory that is required to run a program to completion. The complexity like this depends on the size of the input data and the function that is used for the input size 'n'.
The time complexity deals with the amount of time required by a program to complete the whole process of execution. The time complexity allows creating optimized code and allowing user to calculate it before writing their own functions. The time complexity can be made such that a program can be optimized on the basis of the chosen method.

Write an algorithm to show the postfix expression with the input given as : a b + c d +*f ? .

The postfix expression deals with the expression where the operators are being written after their operands. The evaluation of these operators is being done from left-to-right. The algorithm that is used to show the input of a b + c d +*f ? is as follows:

Write an algorithm through which the inserting and deleting of elements can take place in circular queue?

Circular queues are very important as it allows the element to circulate. In this queue rear end reaches the end and the first element in the list will become the rear of that queue. In this queue the front element can only become the rear element if and only if front has moved forward in the array. The algorithm that is used to represent it is as follows:
insert(queue,n,front,rear,item)
This procedure inserts an element item into a queue.
1. If front = 1 and rear = n, or if front = rear
+ 1, then:
Write: overflow, and return
2. [find new value of rear]
If front = NULL , then : [queue initially empty.]
Set front = 1 and rear=1.
Else if rear = n, then:
Set rear=1.
Else:
Set rear = rear + 1.
[end of structure.]
3. Set queue[rear] = item. [this inserts new element.]
4.Return to the beginning.

How expression trees are gets represented in data structure?

Expression trees are made up of operands like constants and variable names. The nodes also contain the operators. The tree is a binary tree on which all the binary operations are being performed. It consists of all the nodes consisting of two children. It is possible for a node to consist of only one child and other operators that can be used to evaluate the expression tree. The operator looks at the root value that is obtained by recursive evaluation of the subtrees. The expression tree is being handled to show the relationship between the operator and the operand.

How can a binary tree be represented using the rotation?

Binary tree can have rotations and it can be done by inserting a node in the binary search tree. There is a balancing factor that is required and it will be calculated like height of left subtree-height of right subtree. Each node in this case has 0,1,-1 factor value and beyond that there will be no modification possible to be done in the tree. If the balancing factor comes out to be either +2 or -2 then the tree becomes unbalanced. The rotation allows the tree to be balanced and it can be done with the left rotation and right rotation. The rotation also helps the searching to be quite faster than using any other tree. Using the balance factor a tree can be managed and rotation can be applied to the whole system to adjust and balance the tree.

What is the difference between B tree and Binary search tree?

Binary tree consists of only fixed number of keys and children, whereas B tree consists of variable number of keys and children. Binary tree keys are stored in decreasing order, whereas B tree consists of the keys and children in non-decreasing order.
Binary tree doesn't consists of associated child properties whereas B tree consists of keys has an association with all the nodes with the keys that are less than or equal to the preceding key. Binary tree doesn't have minimization factor concept, whereas B tree has the concept of minimization factor where each node has minimum number of allowable children.

What is the minimization factor and time complexity of B-tree?

The minimization factor of every node consists of minimum number of children and they should have at least n-1 keys. There are possibilities that the root node might violate certain properties that are having fewer than n-1 keys. By seeing this every node can have at most 2n-1 keys or 2n children. The height of the n key B-tree can be found out by keeping the minimum degree n<=2, and height as h=logt (n+1/2). The time complexity of this will be given in Big O notation that is the amount of time required to run the code to the completion. The upper bound of the B-tee is provided by this and the lower bound can also be the same. So, mathematically

How does Threaded binary tree represented in Data Structure?

Threaded binary tree consists of a node that is in the binary tree and having no left or right child. The child that comes in the end is also called as leaf node then if there is no child present, it will be represented by the null pointers. The space that is occupied by null entries can be used to store valuable information about the node that is consisting of the child and the root node information. There is a special pointer that is used to point to the higher node in the tree also called as ancestor. These pointers are termed as threads and the whole representation is called as threaded binary tree. The binary tree can be represented in in-order, pre-order and post-order form. Every node in this type of tree doesn't have a right child. This doesn't allow the recursion of the tree.
The code that is used to show the implementation is:

Explain the sorting algorithm that is most suitable to be used with single linked list?

The sorting algorithm that is most suitable with the single link list is the simple insertion sort. This consists of an array and link of pointers, where the pointers are pointing to each of the element in the array. For example: l[i] = i + 1 for 0 < = i < n-1 and l[n-1] = -1.
The linear link list can be pointed by the external pointer which initialized it to 0. To insert the nth element in the list the traversing time gets reduced and until the list is being sorted out completely the process doesn't end. The array that has to be traversed x[k] to sort the element and put them in the list. If the sorting is done then it reduces the time of the insertion of an element and time for searching for a particular element at proper position.

What are the standard ways in which a graph can be traversed?

There are two standard ways through which a graph can be traversed and these are:
1. The depth-first traversal: allow the graph to be traversed from a given point and then goes to the other points. The starting position is being defined as it doesn't consist of any root so, there is a specific point that is chosen to begin the traversing. In this the visits takes place at each vertex and then recursive action is taken to visit all the vertices adjacent to the node that is being visited. The graph can consists of cycles, but there is always a condition that the vertex has to be visited only once.
2. The breadth-first traversal: allow the graph to be traverse one level by another level. Breadth-first visits all the nodes from the depth 0 and it consists of a root. The vertex that has to be visited has to be specified that will be traversed. The length of the vertex has to be defined to find the shortest path to the given vertex. Breadth-first traverse the starting vertex and then all the vertices that is been adjacent to it.

How helpful is abstract data type of data structures?

Abstract data type allows the user to write the code without even worrying about the type of data being used. It is a tool that specifies the logical properties of the data type. ADT is a type consisting set of operations that are called as interface. This interface is the only mechanism through which the data type can be accessed. It defines the new type of instance that is been created by operating on different data types. There is always some additional information on which ADT acts upon. It specifies the instance of the creation time.
The abstract data type can be declared as:

How to sequentially represent max-heap?

Max heap is also known as descending heap consisting of the objects in a heap list with some keys. It is of size n and will be of the form of complete binary tree that is also of nodes n. In this max-heap each node is less than or equal to the content of its parent.
It represents the sequential complete binary tree with the formula to calculate as:Max-heap contains the root element as the highest element in the heap and from there the descending elements will be shown on the children node. It will also be traversed in an orderly manner and will be accessed by accessing the root first then their children nodes.

Write an algorithm to show the reverse of link list?

Link list is a data structure that is commonly used in programming. It is the simplest form. In this each node consists of a child node and a reference to the next node i.e. a link to another node. In this the group of nodes represents a sequence that helps in traversing of the node in an easy manner. The program is given to show the reversing of the link list:

Write an algorithm to show various operations on ordered list and arrays

Ordered list is a container holding the sequence of objects. In this each object is having a unique position in a particular sequence. The operations that are being provided and performed on the ordered list include:
FindPosition: is used to find the position of the object in an ordered list.
Operator[]: is used to access the position of the object in the ordered list.
withdraw(Position&): is used to remove the object from a given position in an ordered list.
InsertAfter: is used to insert an object after some other object or on some position in the ordered list.
InsertBefore: is used to insert the object in an ordered list at a defined position in an array of the ordered list.

Write a program to show the insertion and deletion of an element in an array using the position

To insert the element or delete the element, there is a requirement to find out the exact location as array is a group of linear characters, so it is very important to find the position of the element in an array before performing the actions on them. The program explains the insertion and deletion operations performed on an array of elements:

Write an algorithm to show the procedure of insertion into a B-tree?

The procedure or the algorithm to insert an element into a B-tree is as follows:
1. There is a search function that is applied to find the place where there is any new record to be present. When there is any key inserted then there is a sorting function that works to put the elements in the sorted order.
2. Then a particular node is selected and checked that is there any way to insert the new record. If there is any way to insert the new record then an appropriate pointer being given that remains one more than number of records.
3. If the node overflows due to the increase in the size of the node and upper bound, then there is a splitting being done to decrease the size of that particular node.
4. The split will occur till all the records are not accommodated properly at their place. There can be a way to split the root as well to create the provision for the new record data.

Write an algorithm that counts number of nodes in the circular linked list

Circular linked list is a list in which the insertion and deletion can be done in two ways. There is a provision to count the number of nodes just by keeping a count variable to count the data that is being inserted in the circular list. The algorithm is given to show the count of the nodes in the circular linked list.

Keep a circular header list in memory.
Keep a count to traverse the whole list and to keep a count of the data element
set COUNT: = 0
1. Set PTR: = LINK [START]. {Initializes the pointer PTR}
2. Repeat steps 3, 4, 5 while PTR = START;
3. COUNT = COUNT + 1
4. Set PTR = LINK [PTR]. [PTR now points to next node]
[End of step 2 loop]
5. Exit

Why Boundary Tag Representation is used?

Boundary tag representation is used to show the memory management using the data structures. The memory is allocated from a large area where there is free memory available. Memory management allows the use of segment and process of allocation of resources. This allows the reservation of block of 'n' bytes of memory and a space that is larger than the space of the system. Some tasks are performed like identifying and merging of free segments that has to be released. The process of identification is simpler as it only allows the location of the preceding segment to be located and used. The identification is done to find out the neighbors using the “used/free” flags that are kept with the location. There has to be kept some information regarding the processes and the resources that has been allocated to the data element. It allows the finding of the segment that is to find both the segments (start and end) to be used as a part of boundary tag.

What does Simulation of queues mean?

Simulation is a process of forming and abstract model of the real world situation. It allows understanding the effect of modification and all the situations that are relation to the queues like its properties. It allows the arrangement of the simulation program in a systematic way so that events can occur on regular basis. This allows the transaction to be done on time, for example suppose there is a person p1 submitting a bill and there has to be a period of time that will be take to process his request. If there is any free window then the person can submit the bill and spend less time in the queue. If there is no free availability then there will be a queue. The person has the option to choose the shortest queue to get his work done quickly, but he has to wait until all the previous transactions are processed. This is the way simulation of the queue works.