|
Video on Chain Rule - shortcuts, tips and tricks
Chain RulePoints to Remember
1) Direct Proportion: Any two quantities are said to be directly proportional, if on the increase of one quantity, the other quantity increases and vice-versa.
Example: Cost is directly proportional to number of objects
Cost ∝ Number of objects
Number of objects increases (↑) Cost (↑)
Example: Work done is directly proportional to number of working men
Work done ∝ Number of working men
Number of men increase (↑) Work done (↑)
2) Indirect Proportion: Any two quantities are said to be indirectly proportional, if on the increase of one quantity, the other quantity decreases and vice-versa.
Example: If speed of car is increases, then the time required to cover the distance decreases.
Speed of car (↑) Time required decreases (↓)
Example: Time taken to finish work increases, if number of men decrease.
Time (↑) Number of men (↓)
Tips and Tricks
In this chapter generally different types of numerical related to time and work, time and speed, cost and number of articles, men and work, etc. are asked.
Type 1: Indirect proportion
Q 1. If 30 men can do a piece of work in 20 hours, then in how many hours will 12 men do it?
a. 18 hours
b. 30 hours
c. 40 hours
d. 50 hours
View solution Correct Option: (d)
Hint: As number of workers increase, the time required decreases. Hence, this is a problem related to indirect proportion.
Workers (↑),Time (↓)
Let the number of hours be x.
12 : 30 :: 20 : x 12 men require 50 hours to complete the same work.
Q 2. 3 pumps, working 4 hours a day, can empty a tank in 2 days. How many hours a day must 4 pumps work, to empty the tank in one day?
a. 7 hours
b. 8 hours
c. 6 hours
d. 5 hours
View solution Correct Option: (c)
Hint: As number of pumps increase, the time required decreases and when working hours increase, fewer days are required to complete the work. Hence, this is a problem related to indirect proportion.
Given: 3 pumps can empty a tank in 2 days, if they are working 6 hours a day
Find: Number of hours a day, 3 pumps must work, to empty the tank in one day.
More pumps (↑),Less working hours (↓)
More working hours (↑),Less days (↓) | 4 : x :: | 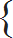 | Pumps are in the ratio 4 : 3 | | Days are in the ratio 1 : 2 |
4 × 3 × 2 = 4 × 1 × x 24 = 4x x = 6 Alternate solution 1: (Trick)Arrange all given parameters in table format. | Pumps | Days | Hours | | 3 | 2 | 4 | | 4 | 1 | ’A’ hrs |
Simply multiply, we get 3 × 2 × 4 = 4 × 1 × A | A = | 3 × 2 × 4 | = 6 hrs | | 4 × 1 |
Alternate solution 2:We are given that, 3 pumps, working 4 hours a day, can empty a tank in 2 days. Therefore, it means that: 3 pumps take total 8 hours to empty the tank. Hence, 1 pump will take 8 x 3 = 24 hours Remember: As number of pump decrease, time required increases. So, if 4 pumps work, time required decreases.
Q 3. A wheel that has 6 cogs is meshed with a larger wheel of 12 cogs. If the smaller wheel has made 22 revolutions, then find the number of revolutions made by the larger wheel.
a. 11
b. 13
c. 15
d. 17
View solution Correct Option: (a)
Hint: As number of cogs increase, the revolutions made decrease. Hence, this is a problem related to indirect proportion.
Let the number of wheels be x.
More cogs (↑),Less revolutions (↓)
Given: 6 cogs meshed with wheel of 12 cogs and smaller wheel made 22 revolutions
Therefore,
12:6 :: 22:x
12 × x=6 × 22
|
|
Type 2: Direct proportion If 30 men can build a wall 56 meters long in 5 days, what length of a similar wall can be built by 40 men in 3 days? a. 36.5 m b. 44.8 m c. 62.3 m d. 92 m View solution Correct Option: (b)
Hint: If more men work, length of wall built is more. If worked for few days, the length of wall built is also less. Hence, this problem is related to direct proportion.
The two main parameters are man and days.
Therefore, | 56 : x :: | 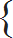 | 30 : 40 - - - (Men) | | 5 : 3 - - - (Days) |
30 × 5 × x = 40 × 3 × 56 | x = | 40 × 3 × 56 | = 44.8 | | 30 × 5 |
5 mat-weavers can weave 5 mats in 5 days. At the same time, how many mats would be woven by 10 mat- weavers in 10 days? a. 10 mats b. 15 mats c. 20 mats d. 30 mats View solution Correct Option: (c)
Hint: More mats are weaved if more weavers work. Hence, this problem is related to direct proportion.
Let the required number of mats be x.
Total 5 mats can be weaved in 5 days by 5 weavers. | 5 : x :: | 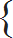 | 5 : 10 - - - (Weavers) | | 5 : 10 - - - (Days) |
5 × 5 × x = 10 × 10 × 5 | x = | 10 × 10 × 5 | = 20 | | 5 × 5 |
20 mats can be weaved in 10 days by 10 mat weavers. If 8 men can reap 40 hectares in 12 days, then how many hectares can 30 men reap in 20 days? a. 175 hectares b. 225 hectares c. 250 hectares d. 275 hectares View solution Correct Option: (c)
Let the required number of hectares be x.
More men (↑) More hectares (↑) | 40 : x :: | 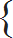 | 8 : 30 - - - (Men) | | 12 : 20 - - - (Hectares) |
8 × 12 × x = 30 × 20 × 40 | x = | 30 × 20 × 40 | = 250 Hectares | | 8 × 12 |
|
|
Type 3: Combination of Direct and Indirect proportion If 3 spiders make 3 webs in 3 days, then 1 spider will make 1 web in how many days? a. 1 day b. 1.5 days c. 3 days d. 6 days View solution Correct Option: (c)
Indirect proportion: Less spiders (↓) More days (↑)
Direct proportion: Less webs (↓) Less days (↓)
We are given, that 3 spiders make 3 webs in 3 days. This means that 3 spiders make a web in each day. 3 days for 3 webs. Hence, work done by each spider is 1/3.
Now a complete web by a single spider can be done by working for 1/3rd each day.
1st day spider will work for 1/3rd
2nd day = 1/3rd
3rd day = 1/3rd
Therefore one complete web can be made in = 1/3 + 1/3 +1/3 = 3/3 = 1 complete web
This means a spider took 3 days to complete 1 complete web. In a diary farm, 20 cows eat 20 bags in 20 days. In how many days one cow will eat one bag of husk? a. 10 days b. 1/10 days c. 20 days d. 40 days View solution Correct Option: (c)
Indirect proportion: Less cows (↓) More days (↑)
Direct proportion: Less bags (↓) Less days (↓)
| 20 : x :: | 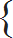 | 1 : 20 - - - (Cows) | | 20 : 1 - - - (Bags) |
1 × 20 × x = 20 × 1 × 20 | x = | 20 × 20 × 1 | = 20 Days | | 20 × 1 |
18 men bind 900 books in 10 days. Find how many binders will be required to bind 600 books in 12 days? a. 10 b. 11 c. 13 d. 15 View solution Correct Option: (a)
We have to find the number of binders. Let the number of binders be x.
Direct Proportion:Less Books (↓),Less binders(↓)
Indirect Proportion:More days (↑),Less binders (↓)
| 18 : x :: | 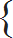 | 900 : 600 - - - (Books) | | 12 : 10 - - - (Days) |
x × 900 × 12 = 18 × 600 × 10 | x = | 18 × 600 × 10 | = 10 | | 900 × 12 |
|
Pipes and Cisterns - Aptitude test, questions, shortcuts, solved example videosPipes & Cisterns - Quantitative aptitude tutorial with easy tricks, tips, short cuts explaining the concepts. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests and competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers, software developers taking entrance exams. Learn and take practice tests!
Boats and Streams - Aptitude test, questions, shortcuts, solved example videosBoats and Streams - Quantitative aptitude tutorial with easy tricks, tips, short cuts explaining the concepts. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests and competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers, software developers taking entrance exams. Learn and take practice tests!
Alligation or Mixtures - Aptitude test, questions, shortcuts, solved example videosAlligation or Mixtures - Quantitative aptitude tutorial with easy tricks, tips, short cuts explaining the concepts. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests and competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers, software developers taking entrance exams. Learn and take practice tests!