Video on Compound Interest - shortcuts, tips and tricksCompound Interest
Points to Remember1) Compound Interest: It is the interest added to the principal of a loan or deposit, so that the added interest also earns interest. This process is called compounding and can also be referred as
“interest on interest”. The interest rate and frequency of compounding which may be
yearly, half yearly, quarterly, monthly, daily, etc. must be specified to accurately define the final amount to be paid with interest.
2) Effective annual rate: A sum of Rs. 100 is borrowed at R % per annum. If compound interest is reckoned quarterly or half yearly, then compound interest rate for 1 year is called as effective annual rate.
3) Principal: It is the money borrowed or lent out for a certain period of time.
4) Interest: Rate of money paid regularly for using money on lent.
Concept of compound interest A person borrows Rs. 2000 at 10 % compound interest. Find the total amount paid by him after 3 years.1) This concept can be easily understood with the diagram shown below. In this case, what happens is, when 10 % interest is applied on the principal, the amount for the first year increases to Rs. 2200.
2) As shown in the figure, finally after 3 years, the total amount to be paid is Rs. 2662.
3) The amount at the end of a 1st year is the principal for the second year and the amount at the end of the 2nd year is the principal for the 3rd year.
4) But in the case of simple interest, the amount after 3 years would be Rs. 2600.
[Simple interest = (PRN/100)] Important Formulae:
Important Formulae: Principal = P, Rate = R % per annum, Time = n years
| 1. Amount = P |  | 1 + | R |  | n | - - - - - - - - - [Interest compounded annually] |
| 100 |
| 1. Amount = P |  | 1 + | (R/2) |  | 2n | - - - - - - - - - [Interest compounded Half-yearly] |
| 100 |
| 1. Amount = P |  | 1 + | (R/4) |  | 4n | - - - - - - - - - [Interest compounded quarterly] |
| 100 |
Quick Tips and Tricks1) Numerical on population:
a) If population of a city is P
1 and it increases by R % annually, then population after n years is given by:
| P2 = P1 |  | 1 + | R |  | n |
| 100 |
b) If population of a city is P1 and it decreases by R % annually, then the population after n years is given by:
| P2 = P1 | 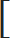 | 1 – | R | 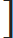 | n |
| 100 |
| 2) If interest is compounded annually and time is in fraction say 2 | 3 | years |
| 5 |
| Amount = P | 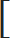 | 1 + | (3/5)R | 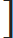 | n | - - - - - - - - - [Interest compounded annually] |
| 100 |
3) If rates are different for different years
(R1 % for 1st year, R2 % for 2nd year, R3 % for 3rd year---- Rn for n years) | Amount for n years = P | 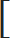 | 1 + | R1 | 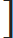 | 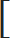 | 1 + | R1 | 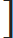 | 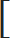 | 1 + | R1 | 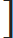 |
| 100 | 100 | 100 |
4) Present worth of sum of Rs. X due n years, hence R % p.a. compound interest is given by:
| Present worth = | |
| X |
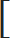 | 1 + | R | 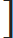 | n | | 100 |
|
5) If difference between compound interest and simple interest is given for:
a) Two years
| C.I. – S.I. = P | 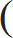 | R | 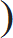 | 2 |
| 100 |
b) Three years
| C.I. – S.I. = P | 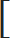 | R2 | 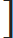 | × | 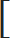 | (300 + R) | 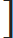 |
| 1002 | 100 |
6) Rule of 72: This rule is used to find:
a) Time required for an amount to double itself, at a given rate of interest.
| Time = | 72 |
| Rate of interest |
b) Rate at which an amount doubles itself in given time.
| Rate of interest = | 72 |
| Time |
Note: The rule of 72 is derived as follows:
We know the general formula to calculate total amount.
| Future value = Present value | 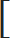 | 1 + | R | 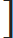 | n |
| 100 |
But when we have to calculate time required for an amount to double itself, at a given rate of interest, the above expression can be written as follows:
Future value (Final amount) = 2 Present value
| Future value | = 2 |
| Present value |
| 2 = | 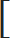 | 1 + | R | 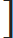 | n |
| 100 |
Using rule of logarithm, we get
| Time = | 72 |
| Rate of interest |
Types of numerical in this chapter: In this chapter there are basically 4 types of numerical. Understanding and studying the concepts clearly will help in solving numerical on this chapter. Type 1: Numerical based on population
The population of a city increases 5 % annually but decreases by ¼ % due to emigration. Find the net increase in percent in 3 years.
A. 8.63 %
b. 11.89 %
c. 13.25 %
d. 14.93 %
View solution Correct Option: (d)
Hint: If population of a city is P1 and it increases by R % annually, then population after n years is given by:
| P2 = P1 | 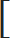 | 1 + | R | 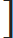 | n |
| 100 |
Solution: We are given that, the population of a city increases 5 % annually but decreases by ¼ % due to emigration.
Assume original population of the city = 100
1) Increase in population = 5 %
2) Decrease in population due to emigration = ¼ %
Hence, net annual increase = 5 % - ¼ % = 19/4 %
Therefore,
| Population in 3 years = P2 = P1 | 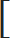 | 1 + | R | 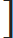 | n |
| 100 |
| = 100 | 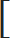 | 1 + | 19 | 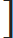 | 3 |
| 4 × 100 |
| = 100 × | 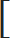 | 419 | 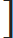 | 3 |
| 400 |
=114.93
Population after 3 years will be 114.93 and at present it is 100. Therefore,
Increase in population = 114.93 – 100 = 14.93 %
The value of a sewing machine depreciates at the rate of 10 % after every year. If at the end of 3 years, its value is Rs. 8748, then find its purchase price.
a. 8000
b. 10000
c. 12000
d. 15000
View solution Correct Option: (c)
Hint: If cost of a machine is P1 and it decreases by R % annually, then the purchase price after n years is given by:
| P2 = P1 | 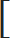 | 1 – | R | 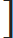 | n |
| 100 |
We are given that the value of a sewing machine depreciates at the rate of 10 % after every year. After 3 years, its value is Rs. 8748.
| 8748 = P1 | 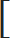 | 1 – | 10 | 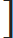 | 3 |
| 100 |
P
1 =Rs.12000
Purchase price of the sewing machine = Rs. 12000