Video on Clocks
"A mechanical or electrical device for measuring time, indicating hours, minutes, and sometimes seconds by hands on a round dial or by displayed figures."
Hour hand is also known as
Short hand because it is smaller hand in Clock.
Minute hand is also known as
Long hand because it is larger hand in Clock.

Questions are asked on mechanical type of clock (Not from digital clock/watch).
Importance of topic
These types of questions are asked in IBPS PO, IBPS Clerk, CMAT, GMAT, CAT, SSC CGL, Clerical, CET, etc.
Key Points
A. The dial of the clock is circular in shape and is divided into 60 equal parts, called
minute spaces.
B. 60 minute spaces trace an angle of 360°.
C.
In 1 hour, Minute hand traverses
60 minute space or 360° degree, Hour hand traverses
5 minute space or 30° degree.
In 1 minute, Minute hand traverses 6° (dpm – Degree per Minute),
Hour hand traverses
0.5° (dpm – Degree per Minute).

D. The hands of the clock are perpendicular in 15 minute spaces, at that time two angle are at right angle (90°).

E. The hands of the clock are perpendicular to each other for 22 times in 12 hours and for 44 times in a day (Because between 2, 3 and 3, 4 and 8, 9 and 9, 10 hands of the clock are not perpendicular to each other).
F. The hands of the clock are in straight line when they coincide or opposite to each other for 44 times in a day.
G. The hands of the clock are in straight line and opposite to each other in 30 minute spaces apart (180°).

H. The hands of the clock are opposite to each other for 11 times in 12 hours and 22 times in a day (Because between 5, 6 and 6, 7 hands of the clock are not opposite of each other).
I. Between every two hours the hands of the clock coincide with each other for one time except between 11, 12 and 12, 1. In a day they coincide for 22 times.

J. The minute hand gains 55 minutes over hour hand per hour.
K. The hands overlap about every 65 minutes, not every 60 minutes.
L. If a watch or a clock indicates 2:20, when the correct time is 2, it is said to be 20 minutes fast.
M. On the other hand, if it indicates 1:40, when the correct time is 2, it is said to be 20 minutes slow.
N. If the real time is given and its MIRROR image is asked or vice – versa, simply subtract the given time from 11:60.
For example the time is 10:10 in the mirror then subtracting it from 11:60 we get 1:50 which will be the mirror image of the clock.
[This is a very useful and time saving shortcut for exam and is rarely available in the books which increases its importance]

O. A broken clock is right twice a day. However, a clock which gains or loses a few minutes might not be right twice a day or even once a day. It would be right when it had gained / lost exactly 12 hours.
General terms used in clock:
| Terms | Time |
|---|
| Fifteen minutes past seven | 7:15 |
| Twenty minutes to eight | 7:40 |
| Quarter past six | 6:15 |
| Quarter to six | 5:45 |
| Half past six | 6:30 |
| Nine o’clock | 9:00 |
| Noon or Midday | 12:00 |
| AM/am/A.M./a.m. | After Meridiem |
| PM/pm/P.M./p.m. | Post Meridiem |
Types of Questions
1) Angle Between the Hands of clock
Examples
i) What is the angle between the hands of the clock at 3:40?
a) 240°
b) 110°
c) 130°
d) 190°
View solution Correct Option: (c)
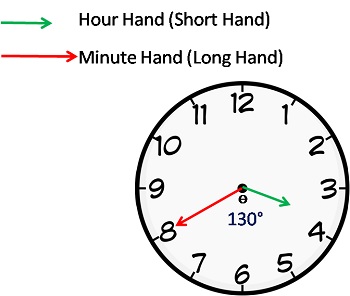
At 3 o’ clock, the hour hand is at 90 degrees from the vertical.
In 40 minutes,
Hour hand = 90 + 40*(0.5) = 90 + 20 = 110 (The hour hand moves at 0.5 dpm)
Minute hand = 40*(6) = 240 (The minute hand moves at 6 dpm)
Difference or angle between the hands = 240 – 110 = 130 degrees.
a) 160°
b) 180°
c) 150°
d) 190°
View solution Correct Option: (a)
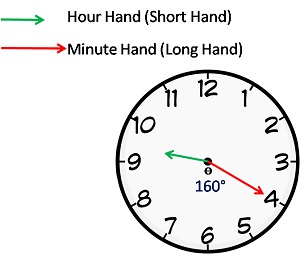
At 9 o’ clock, the hour hand is at 270 degrees from the vertical.
In 20 minutes,
Hour hand = 270 + 20*(0.5) = 270 + 10 = 280 (The hour hand moves at 0.5 dpm)
Minute hand = 20*(6) = 120 (The minute hand moves at 6 dpm)
Difference or angle between the hands = 280 – 120 = 160 degrees.
a) 215
b) 180
c) 210
d) 195
View solution Correct Option: (a)
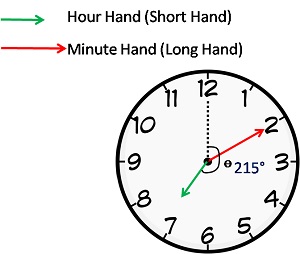
In a clock, 12 hours form 360° degree. So one hour forms 30°. Therefore 7 hours form 210° (30° X 7) degree.
In a minute, hour hand moves 0.5° degree, so in 10 minutes it moves 0.5° X 10 = 5°
Thus, by 10 Minutes past 7, hour hand has turn through 210° + 5° = 215°
a) 25°
b) 150°
c) 50°
d) 300°
View solution Correct Option: (a)
The speed of hour hand is 0.5 dpm (Degree per Minute)
And the speed of minute hand is 6 dpm.
So, 300 degree traverse by minute hand in 300/6 = 50 Minutes.
Thus, angle moved by the hour hand in 50 minutes is 50/0.5 = 25° degrees.
a) 1:25
b) 12:35
c) 1:35
d) 12:25
View solution Correct Option: (b)
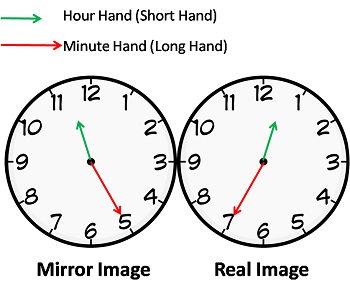
Shortcut is to subtract the given time from 11:60 (As mentioned in key Point N). Thus the correct time is 11:60 – 11:25 = 0:35 and 0:35 mean 12:35 So, Answer is 12:35.
a) 10:50
b) 11:50
c) 12:50
d) 1:50
View solution Correct Option: (b)
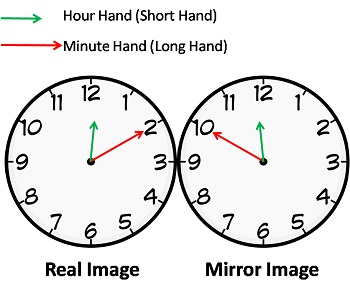
Shortcut is to subtract the given time from 11:60 (As mentioned in key Point N). Thus the correct time is 11:60 - 00:10 = 11:50 because 12:10 mean 00:10.
a) 11:08
b) 12:38
c) 11:38
d) 12:08
View solution Correct Option: (c)
8 Seconds in 4 Minutes mean 120 Seconds (or 2 Minutes) in one hour.
From 4AM to 11PM (on the same day) = 19 hours
So, total seconds gain in 19 hours = 19 X 120 (Seconds gain per hour) = 2280 Seconds.
Now, 2280 Seconds = 38 Minutes (i.e. 2280/19 = 38)
Thus incorrect clock will show 11:38PM at 11PM.
a) 11AM on Sunday
b) 11AM on Monday
c) 11AM on Tuesday
d) 11AM on Wednesday
View solution Correct Option: (a)
As mentioned in Key Point O, faulty clock will show correct time when it loses or gains 12 Hours.
In the given problem, clock loses 5 Minutes in an hour. So, 1 Minute lost in every 12 minutes (60 minutes / 5 minutes = 12 minutes).
Now, for losing 12 hours i.e. 720 Minutes(12 X 60 = 720) it will take 720 X 12 = 8640 Minutes = 144 Hours = 6 Days.
So, Clock will show correct time after 6 days from 11AM Monday.
Thus, Answer is 11AM on Sunday.
a) Wednesday noon
b) Sunday 2PM
c) Monday noon
d) Tuesday 2PM
View solution Correct Option: (d)
At noon on Sunday watch gains 2 Minutes.
And at 2PM on following Sunday it is 4 Minutes 48 Seconds fast.
So, it gains 6 Minutes 48 Seconds i.e. 2 Minutes + 4 Minutes 48 Seconds (total 408 Seconds) in 170 Hours (Hours from Sunday Noon (12PM) to following Sunday 2PM)
Therefore, watch gains 120 Seconds (2 Minutes) in 170*120/408 = 50 Hours
50 Hours = 2 Days 2 Hours
Thus, Watch was correct after 2 days 2 hours from Sunday noon that is Tuesday 2PM.
a) 20
b) 22
c) 24
d) 48
View solution Correct Option: (b)
Key points – H.
a) 22
b) 44
c) 24
d) 48
View solution Correct Option: (b)
Key points – F. It has not been mentioned coincide or opposite of each other. So, we have to consider common scenario where the hands are in straight line that is either opposite or coincide of each other.
a) 20
b) 21
c) 22
d) 24
View solution Correct Option: (c)
Key Points – I.
a) 22
b) 24
c) 44
d) 48
View solution Correct Option: (c)
Key Points – E.
a) 0.5°
b) 1°
c) 1.5°
d) 3°
View solution Correct Option: (a)
Key Points – C.
a) 6°
b) 30°
c) 5°
d) 36°
View solution Correct Option: (d)
Key Points - C. In a minute, minute hand traverses 6° degree. So in 6 minutes, it traverses 6 X 6° = 36°.
Therefore answer is 36°.