Video on Square Root and Cube Root - shortcuts, tips and tricksSquare root and Cube root
Important points to remember: Square root: If a
2 = b, we say that the square root of b is a
It is written as
b = a
2) Cube root: Cube root of a is denoted as
3a3) ab =
a ×
b| 4) (a/b) = | a | = | a | × | b | = | ab |
| b | b | b | b |
5) Number ending in 8 can never be a perfect square.
6) Remember the squares and cubes of 2 to 10. This will help in easily solving the problems.
Find the numbers which have same digit in unit’s place: 
Quick Tips and Tricks 1) Finding square root of 5, 4 and 3 digit numbers How to find the square root of 5 digit number ? 
How to find the square root of 4 digit number? 
How to find the square root of 3 digit number?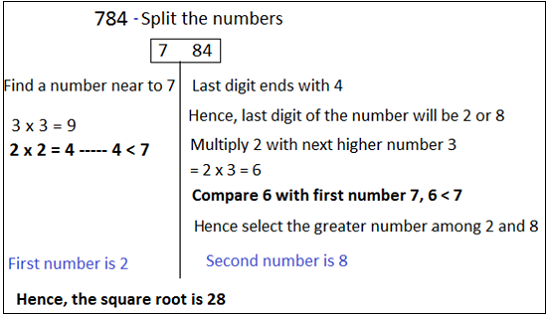 
2) Finding the square of large numbersExample: 47
2 = 2209
Square of 47 can be easily determined by following the steps shown below:
Step 1: Split the number 47 as 4 and 7.
Step 2: Use the formula: (a + b)
2 = a
2 + 2ab + b
2Here, (4 + 7)
2 = 4
2 + 2 × 4 × 7 + 7
2 Without considering the plus sign, write the numbers as shown below:
[16] [56] [49]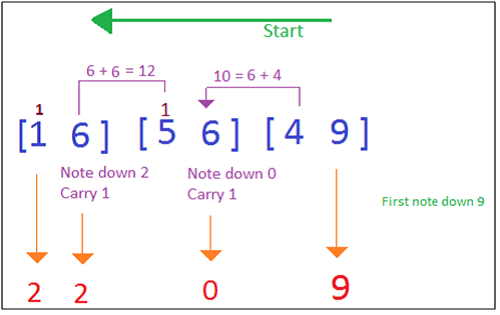 
Step 1: Write down 9 from 49 and carry 4 to 56.
[-----9] Step 2: After adding 4 to 6, we get 10. Therefore, write down zero and carry 1 (5 + 1 = 6) to 16.
[----09] Step 3: 6 + 6 = 12, write down 2 and carry one.
[---209] Step 4: Finally write the answer along with (1 + 1 = 2).
[2209] 3) Finding the cube root of 6 digit number? Note: Cube roots of 6, 5, 4 or 3 digit numbers can be easily found out by using the same trick as used to find the square root of larger digits.
Example: 3132651Remember: The last 3 numbers are to cut off and the nearby cube of first remaining numbers is to be found out. Step 1: Split the number 132 and 651
Step 2: 125 is the cube of 5, which is the closest number to 132. Hence, first number i.e. the number in ten’s place is 5.
Step 3: 1 is the digit in unit’s place. Hence, the digit in unit’s place is 1.
Hence, the cube root of 132651 is 51. 4) How to find a number to be added or subtracted to make a number a perfect square ? For easy understanding, let’s take an example.
Example: 8888
Step 1: Divide 8888 by 9. We get remainder 7.
Step 2: Add Divisor and Quotient [9 + 9 = 18]
Step 3: Now the next divisor will be (18 and number x) which will divide the next dividend.
In this case, 4 is the number x and now the divisor becomes 184 × 4 =736. Step 4: This step is to be followed depend the number of digits in the dividend.
Case 1: If we have to find a
number to be added to make a number
perfect square, then
Consider a number greater than the quotient. Her quotient is 94, hence consider 95.
94
2 < 8888 < 95
28836 < 8888 < 9025Number to be added = Greater number – Given number Number to be added = 9025 – 8888 =
137Case 2: If we have to find a
number to be subtracted to make a number
perfect square, then
94
2 < 8888 < 95
28836 < 8888 < 9025Number to be subtracted = Given number - Smaller number Number to be added = 8888 – 8836 =
52Question VarietyThere are basically 4 types of questions asked from this chapter. Understanding and practicing each of the 4 types will help you deal successfully with the problems from this chapter. Type 1: Find the square root and cube roots of given numbers
Find the square root of 5929
a. 49
b. 33
c. 77
d. 73
View solution Correct Option: (c)
Remember the trick discussed in Quick Tips and Tricks
Step 1: Split the number 59 29
72 = 49 is the nearest number to 59.Hence, the digit in ten’s place is 7.
Step 2: Last digit of number 29 is 9. Therefore, 3 or 7 are the digits in unit’s place.
Multiply 3 by next consecutive higher number i.e. 4
3 × 4 = 12
But 12 < 59, hence consider the largest number among 3 and 7.
The digit in unit’s place is 7.
Hence, the square root of 5929 is 77
Find the cube root of 1728.
a. 12
b. 14
c. 16
d. 18
View solution Correct Option: (a)
Hint: This type of questions can be easily solved by resolving the given number as the product of prime factors and select one common factor among the repeated factors.
The number, 1728 is easily divisible by 2, 4, 8, 12, etc. Selecting the greater number 12 will reduce the taken consumed to solve the problem.
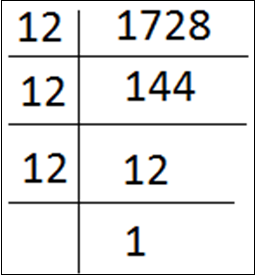
1728 = 12 × 12 × 12 = 123
Find the value of
151a. 12.459
b. 12.292
c. 13.591
d. None of these
View solution Correct Option: (b)
Hint:
Trick to find the square root of numbers which are not perfect squares.
Step 1: Find the closet square to 151. 144 is the closest square, its square root is 12.
Step 2: Now divide the given number by the square root of closest square i.e. 12
Step 3: Take the average of 12.583 and the square root of the closest number.
| 12 + 12.583 | = 12.2915 = 12.292 |
| 2 |
151 = 12.292 is the approximate value upto 3 decimal places Find is the value of
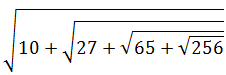
a. 9
b. 8
c. 6
d. 4
View solutionQ 5. Find the value of
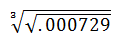
a. 0.3
b. 0.7
c. 0.09
d. None of these
View solution
